作者(Alex Rodriguez, Alessandro Laio)提出了一种很简洁优美的聚类算法, 可以识别各种形状的类簇, 并且其超参数很容易确定.

算法思想

该算法的假设是, 类簇的中心由一些局部密度比较低的点围绕, 并且这些点距离其他高局部密度的点的距离都比较大. 首先定义两个值: 局部密度$$\rho_i$$以及到高局部密度点的距离$$\delta_i$$:

$$ \rho_i=\sum_j\chi(d_{ij}-d_c) $$

其中

$$ \chi(x)= \begin{cases}1 & if x<0\ 0& otherwise \end{cases} $$

$$d_c$$是一个截断距离，是一个超参数。所以$$\rho_i$$相当于距离点$$i$$的距离小于$$d_c$$的点的个数。由于该算法只对$$\rho_i$$的相对值敏感，所以对$$d_c$$的选择比较鲁棒，一种推荐的做法是选择$$d_c$$使得平均每个点的邻居数为所有点的1%-2%。

$$ \delta_i=\min_{j:\rho_j>\rho_i}(d_{ij}) $$

对于密度最大的点，设置$$\delta_i=max_j(d_{ij})$$。注意只有那些密度是局部或者全局最大的点才会有远大于正常的相邻点间距。

##聚类过程

那些有着比较大的局部密度$$\rho_i$$和很大的$$\delta_i$$的点被认为是类簇的中心. 局部密度较小但是$$\delta_i$$较大的点是异常点.在确定了类簇中心之后, 所有其他点属于距离其最近的类簇中心所代表的类簇. 图例如下:

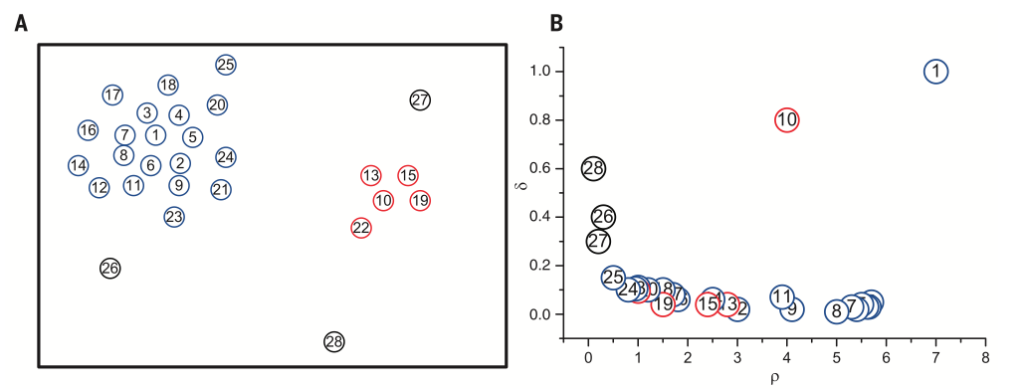
左图是所有点在二维空间的分布, 右图是以$$\rho$$为横坐标, 以$$\delta$$为纵坐标, 这种图称作决策图(decision tree). 可以看到, 1和10两个点的$$\rho_i$$和$$\delta_i$$都比较大, 作为类簇的中心点。 26, 27, 28三个点的$$\delta_i$$也比较大, 但是$$\rho_i$$较小, 所以是异常点。

##聚类分析

在聚类分析中, 通常需要确定每个点划分给某个类簇的可靠性. 在该算法中, 可以首先为每个类簇定义一个边界区域(border region), 亦即划分给该类簇但是距离其他类簇的点的距离小于$$d_c$$的点。 然后为每个类簇找到其边界区域的局部密度最大的点, 令其局部密度为$$\rho_h$$该类簇中所有局部密度大于$$\rho_h$$的点被认为是类簇核心的一部分(亦即将该点划分给该类簇的可靠性很大), 其余的点被认为是该类簇的光晕(halo), 亦即可以认为是噪音. 图例如下:

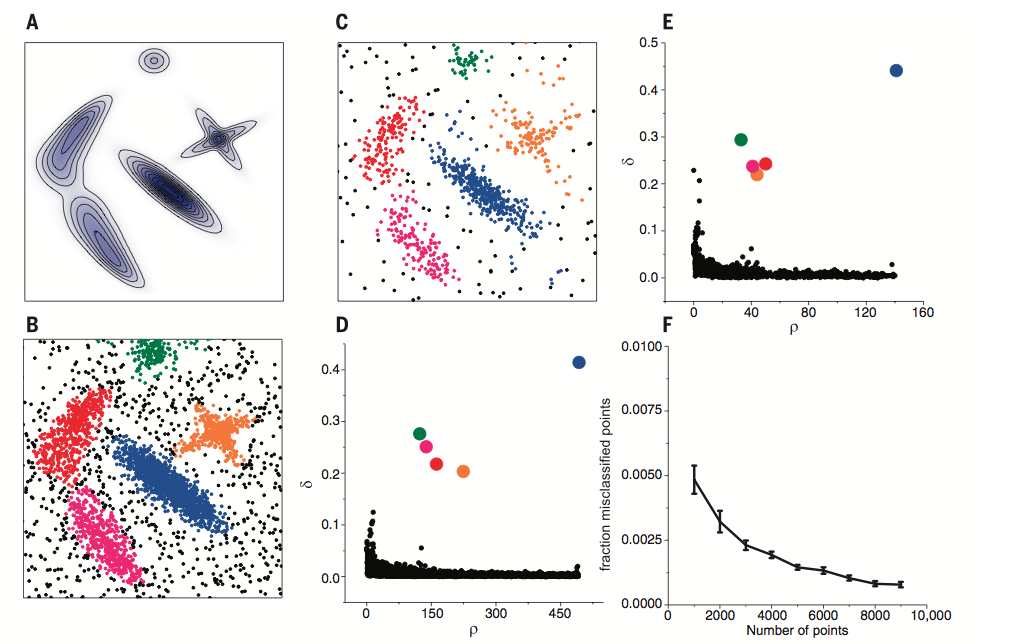
A图为生成数据的概率分布, B, C二图为分别从该分布中生成了4000, 1000个点. D, E分别是B, C两组数据的决策图(decision tree), 可以看到两组数据都只有五个点有比较大的$$\rho_i$$和很大的$$\delta_i$$。 这些点作为类簇的中心, 在确定了类簇的中心之后, 每个点被划分到各个类簇(彩色点), 或者是划分到类簇光晕(黑色点)。F图展示的是随着抽样点数量的增多, 聚类的错误率在逐渐下降, 说明该算法是鲁棒的。

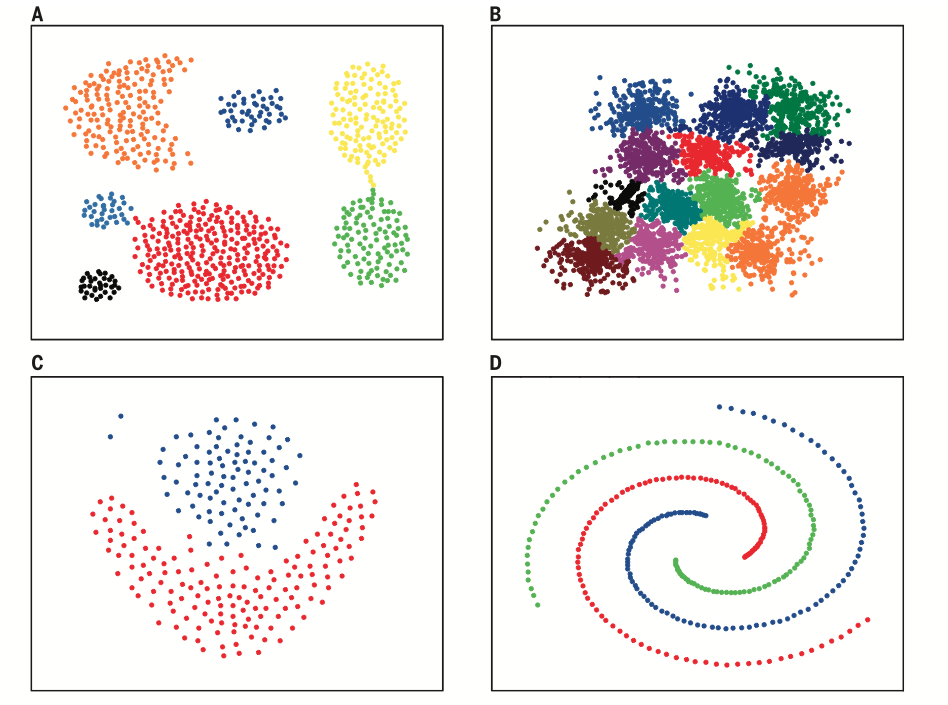
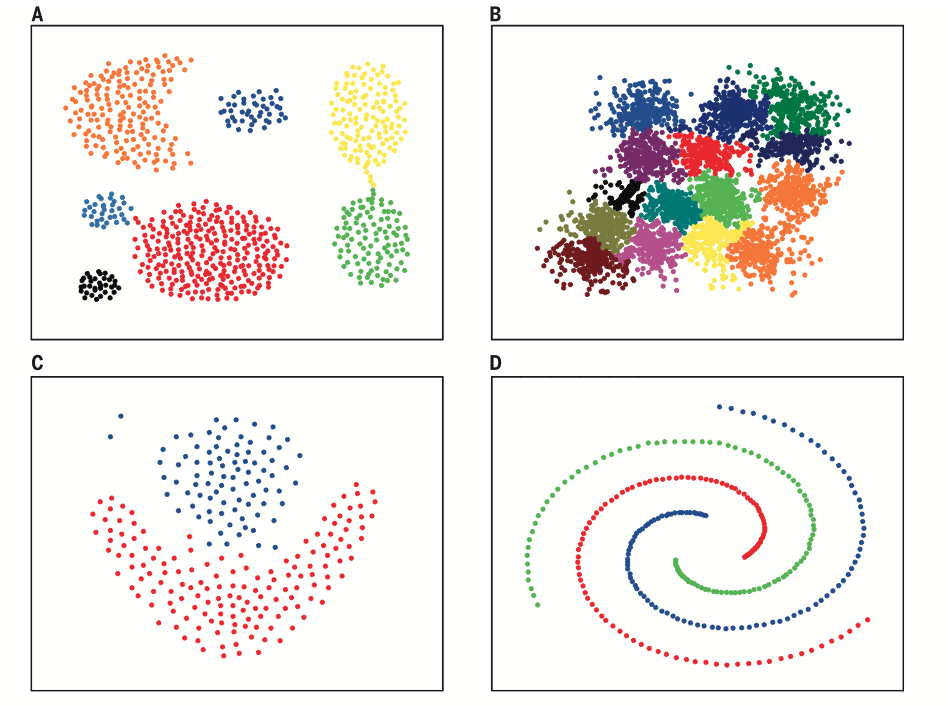
最后展示一下该算法在各种数据分布上的聚类效果，非常漂亮。

参考文献:

[1]. Clustering by fast search and find of density peak. Alex Rodriguez, Alessandro Laio

本文转载自Kemaswill’s Blog

欢迎关注我的个人公众号：helixminer（碱基矿工）